Network Calculus and Optimization

Project Description

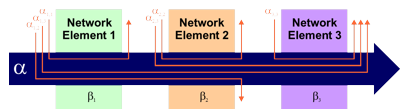
Logo network_calculus

Network calculus (NC) is a system theory for deterministic performance evaluation. It uses mathematical methods to provide performance guarantees for communication systems. It can be applied in the design phase of future systems as well as the analysis of existing systems. In real-time systems, the timeliness of events plays an important role. Therefore, the classical performance evaluation based on stochastic methods that result in (stochastic) expectation values, i.e. mean values, has to be extended by mathematical tools producing guaranteed bounds for worst case scenarios. Network calculus allows to obtain upper bounds for end-to-end delays for one nodes or a series of nodes within a network, upper bounds for the required buffer space and bounds for the output flow. These analytic performance bounds characterize the worst-case behavior of traffic flows and allow dimensioning the corresponding systems.

Currently, we study the applicability of NC for multiplexed flows, in particular when the FIFO property cannot be assumed at the merging of individual flows. The aggregation of data flows plays an important role in modelling the multiplexing scheme. We apply NC for performance evaluation both of aggregate multiplexing at one node and at concatenation of aggregated multiple nodes in different scenarios.
We have successfully introduced network calculus methods in the field of internal automotive communication systems in industrial applications. Embedded in-car networks need to fulfill hard real-time constraints. While TDMA-based access schemes in FlexRay guarantee that certain bound can be met, statistical multiplexing in CAN networks only allows to calculate bounds for the highest priority messages. By applying network calculus, we obtained bounds for all priority classes without the need to specify a concrete scheduling of the messages. Upper bounds for the amount of data that arrives at each network node are enough to determine hard bounds for the end-to-end delay in CAN networks.

Another field of application is industrial communication. Factory automation often also requires hard real-time bounds for the end-to-end delay of messages. The use of Ethernet with priority tagging allows cost-efficient implementation of factory automation systems. But without stringent planning of the network, the required bounds on the end-to-end delay cannot be guaranteed. Network calculus allows to obtain the required bounds when applied in the planning phase of the network. It also allows to dimension the buffers of nodes, e.g. of industrial Ethernet switches. Nowadays, some of the users of industrial Ethernet need to integrate non-real-time products like web cams and remote operation terminals into existing networks. Without additional analysis, the additional traffic caused by devices that do not require hard real-time constraints will cause a violation of the bounds for the delay and buffer space for real-time traffic. By taking into account this non-real-time traffic in network calculus and by applying traffic shaping for the non-real-time flows allows to dimension the network so that all bounds are met. Network calculus is currently integrated into an existing automated industrial network planning tool.

Project Period

    2004-03-01 – present

Project Leader

Related Publications

  •